Once the abstract ideas are given a basic form, the artist moves on to the last step of the classical design process enhancing the form by detailing it and adding attributes. Procedures followed for detailing allow full scope for a variety of creative expressions to emerge even when the earlier steps in the design process might appear rigid. This leads to a creation of a variety of unique and intriguing designs that don’t look the same, even when they share the essence. A look at Indian temple architecture (some examples shown in Figure 100) clearly shows that all temples have a unique design and details, even though the basic abstract concepts, mappings and high level metaphors are constant. This is a crucial step owing to the need for constant newness in the contemporary world, where there is a constant demand for something new and appealing.
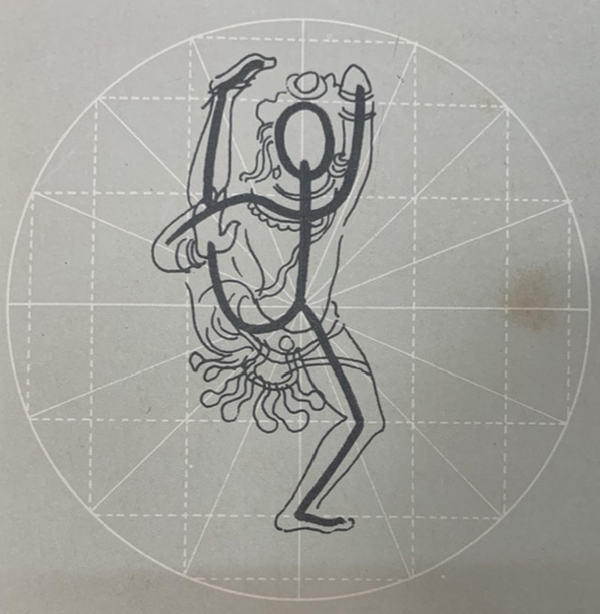
Figure 99: Nataraja Figure with a sense of Dynamism

Figure 100: Indian Temples with Unique Designs
Ways of Detailing Form
There are various procedures and techniques for detailing forms depending on the type of form, inspired from artefacts ranging from architecture to manuscripts. These techniques involved ornamentation, procedures like parametrization, shape and form transitions to get complexity, and so on.
A look back at Figure 70 shows various embellishments used to decorate the text in Jain manuscripts. There are Gold borders that serve to highlight chunks of text. On some pages, these borders are filled with intricate designs of flowers that increase the aesthetic appeal, along with having a symbolic significance. Figure 101 shows how Jain manuscripts called the Kalpasutra use a variety of colours, intricate border ornamentation and hand made patterns to create visually appealing designs. Similar ornamentation can also be seen in the heavily decorated Mughal era writings as shown in Figure 102. A variety of handmade patterns inspired from elements of nature like plants and animals have been used to decorate the text, as can be seen on the margins. The text itself has been given different colours, along with a gold background.

Figure 101: Ornamentation in Jain Kalpasutra

Figure 102: Ornamentation in Mughal Writings
A look at examples from classical Indian architecture sheds light on many ornamentation techniques. Mughal architecture like mosques and mausoleums contains embellishments with a heavy inspiration from elements of nature and geometry, as can be seen in Figure 103 which shows different details on the Taj Mahal. Figure 103 (a) shows a hexagonal Jali design, with small Jalis made of different shapes on top. Figure 103 (b) shows surface embossments inspired from plants and flowers. Figure 103 (c) shows religious text written around the opening, where the text itself is the ornamentation. All details are meaningful, and have a purpose of communicating some abstract idea. No detail is meant to be standalone, just for the purpose of filling up space.

Figure 103: Detailing in Taj Mahal
Similarly, Hindu architecture also contains decorative motifs on temple facades, some examples of which can be seen in Figure 104. These motifs physically as well as conceptually are part of the structure as a whole, and complement the story being told.
Fractals and Parametrization
A way of detailing form that has been heavily employed in classical Indian arts, and is apparent from structures like Hindu temples, is by using fractals. Fractals, in simple terms, are self-similar patterns that are invariant to scaling. This means that they look the same no matter how much one zoom in. They are made by following simple iterative steps over time, which results in extremely rich, unique and non-repetitive forms which could not have been visualised by intuitive means. Nature is full of examples of repetitive patterns that can be classified as fractals, from which Indian arts and architecture are heavily inspired.
Natural objects around us are filled with fractal patterns at multiple levels, ranging from flowers, trees and plants to even coastlines and mountains. Figure 105 (a) shows the branching pattern of a tree. The branching pattern as a whole is self-similar- it repeats until the branches become smaller and smaller, and would look the same when one zoom in. Similar branching can also be seen in lightning strikes and earthquakes. The branching in itself is a recursive process which results in unique nonrepetitive shapes. Figure 105 (b) shows fractals in a flower. Here, the pattern gets increasingly smaller as it repeats towards the center. Since even a small change at this scale can create different patterns, each flower ends up being unique. These changes, or variations, are referred to as parametric variations, and the whole process of making fractals is called parametrization. Fractals need not be always symmetrical, as can be seen in a shoreline in Figure 105 (c). A shoreline, especially a rocky one, exhibits fractal behaviour as it is formed due to natural processes of erosion over a long period of time. It gets more detailed as one zoom in, and this behaviour needs to be kept in mind when one is measuring the length of the coast.

Figure 104: Motifs on Hindu Temples
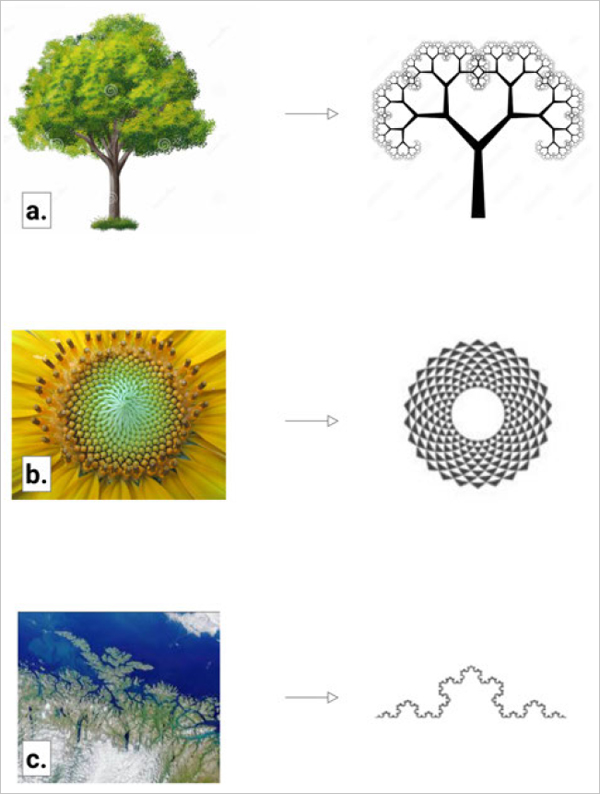
Figure 105: Fractals in Nature
Indian arts, especially architecture, heavily employ fractals to generate detailed and unique forms with constant variations without exact repetition, much like nature. Hindu temples employ self-replication as a method of fractal generation, in which shapes contain smaller replicas of themselves at various scales, as can be seen in Figure 106. Here, the recursive process becomes addition of these self-similar shapes until the shapes keep getting smaller and smaller, to achieve a complex end result. Simple shapes in themselves can be modified or filled up using simple recursive processes to achieve complexity of growth, as can be seen in Figure 108. This growth can happen on the edges, similar to coastlines, or it can happen within the shape to increase detail density. In all kinds of fractal creation, there is a rule which defines what recursive procedure to follow. For example, Figure 107 shows two different fractal patterns made using a scaled self-similar replication of a circular shape. In both the cases, smaller versions of the same circle are added over and over. However, there is a difference in the rule followed to create the fractal, leading to results which are visually vastly different. Similar recursive processes are applied to architectural forms, like temples to create more and more complex variations, as can be seen in Figure 109. The first image shows the detailing done on temple elevations. On the left is the simple form the architect starts with, on which the big details are added. Then, following recursive process, smaller versions of these shapes are added again and again to achieve a complex and detailed elevation, as seen in the right image. A similar technique can be applied to the temple plan, where details are added again and again to simple edges. The third image shows the fractal growth on temple motifs and pillars. Here, the details themselves have replication, providing the temple complexity at multiple levels.
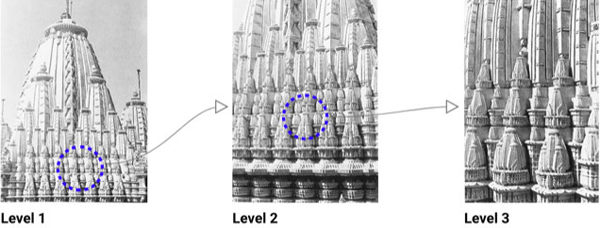
Figure 106: Self replication for Fractal generation in Temples
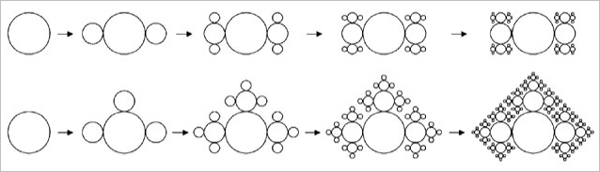
Figure 107: Generating fractals from circle using two different rules

Figure 108: Increasing complexity in simple shapes
Fractal growth can also be imagined in all three dimensions, as can be seen in Figure 110. Here, the process of self-replication by adding smaller and smaller cubes to a bigger cube has been followed to achieve a complex end result.
Shape transitions are another way of adding complexity to form. Circle and square are two of the most important shapes in Indian art, as they are metaphors for order and the continuum of respectively. Indian architecture, especially in temple plans, derives circle from square using various methods. This increases form complexity along with employing both the shapes for their abstract meaning. One approach can be deriving the circle from successive facetting of a square, as can be seen in Figure 111 (a). The size of the square would determine the complexity of the resulting shape. Another approach can be keeping on increasing the number of edges taking the initial shape as a square, as can be seen in Figure 111 (b). The third approach can be rotating a square to get a circular outline, as can be seen in Figure 111 (c). Modifying the parametric variations, such as changing the size of the initial square, its angle of rotation or the number of times it replicates, can result in vastly different end results.

Figure 109: Increasing complexity in Temple architecture
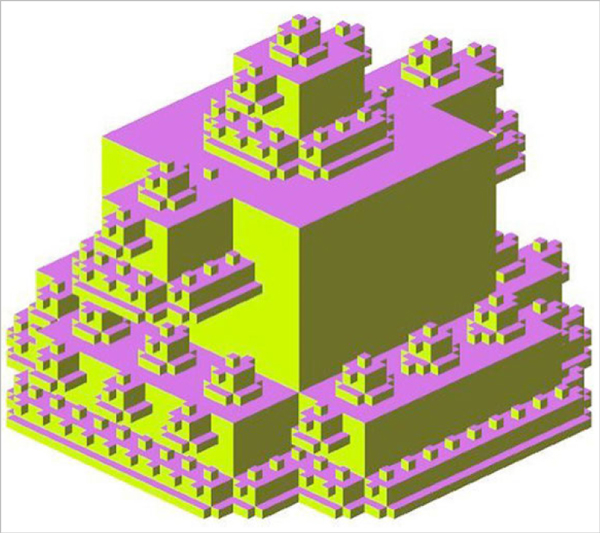
Figure 110: Fractal in 3D
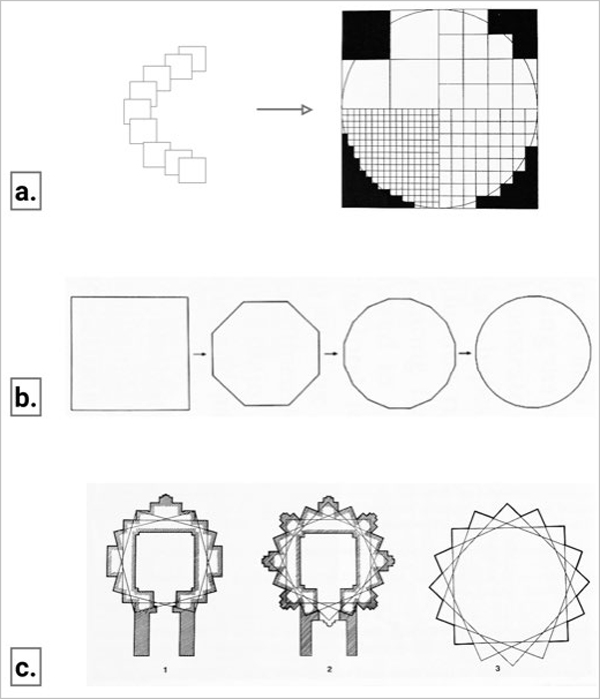
Figure 111: Various approaches to achieve Circularity
Figure 112 shows the facetting technique more clearly. As one increases the number of small squares, the whole outer shape starts looking more and more like a circle, even though it is still made of squares. The number of small squares in this case becomes the parametric variation for this process of converting a square into a circle. This variation leads to many different results just by tweaking the number of squares. Fractals help in making complex forms, but they also help in ornamentation of these forms with complex patterns, the best example of which is Mughal architecture. Figure 113 (a) and (b) show fractal patterns added as ornamentation for ceiling and floor respectively.
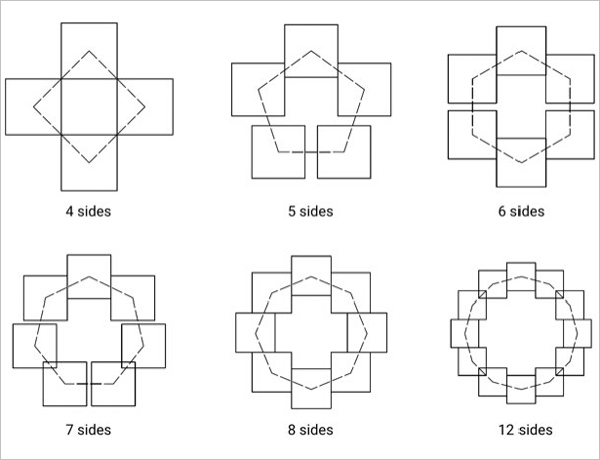
Figure 112: Facetting a square to make a circle

Figure 113: Fractals in Mughal patterns

