Task 07:
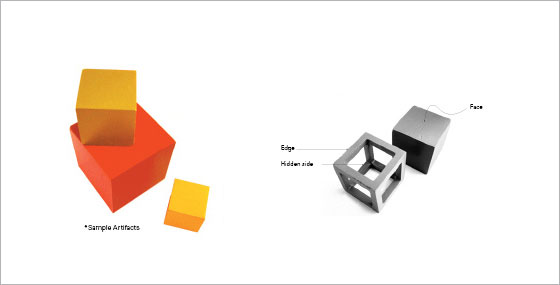
In this exercise, some sample artifacts* will be provided to you. We will draw these artifacts (cubes of various sizes), in different configurations. We would also shift our viewpoints (physically) while drawing them. We may encounter configurations where these opaque cubes would overlap each other and make our task difficult, at times, forcing us to visualize the hidden side.

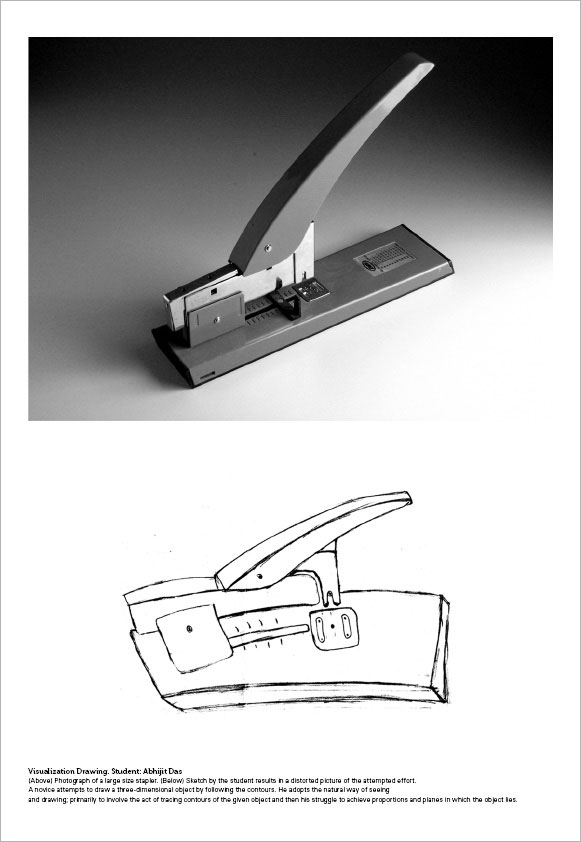
In an opaque object, we can never see the hidden structure (lines or edges) that constitutes a form. Therefore, when we are presented with a complex form (a combination of several forms, e.g. cylinders, cuboids, or pyramids), we usually end up tracing the contours of the form (refer to drawing of a stapler by Abhijit Das ). Whereas, when the form is simple as a cube we prefer to visualize the structure of the form.

To be able to draw a three-dimensional form with precision, a student should go beyond external appearance of the form. He should try to understand the underlying geometry and structure of things. This leads to an argument that while sketching three-dimensional objects why should one attempt to draw them as solids (opaque objects) with hidden faces or edges? Why can't we make them transparent?

Task 08:
The second session of the assignment will provide artifacts which will be transparent. It means the student will be able to see-through the artifact (refer to see through cubes by Nishant Mungali), making it easy for him to understand the structure of such solids. It is important that drawing the structures of cubes and rectangular solids should be practiced regularly, for there begins the foundation to construct other forms (cylinders, pyramids, etc.). To check this fact we will draw cylinders inscribed in the cubes and understand the exercise.

In the last exercise, we learnt how three lines when shaded along their respective planes were perceived as a corner of the cube. A Boolean operation to the modified edge resulted in creation of more faces for the cube. All lines ran parallel along the corresponding faces because the resultant was a cube. It gave us cues to create intrusions along the modified edge. The appropriateness of the modifications was cross- checked with the fact that all lines should be parallel to each other.

Note:
Edges of the cubes form three sets of lines, one vertical and two horizontal, each having its vanishing points in perspective. When we draw objects kept very close to us, the vanishing points of these lines are too far away to converge on paper, we are drawing on. When these vanishing points are made to converge forcibly in the drawing, it looks artificial and more mechanical. (Francis D.K. Ching)1