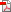Figure 8.3.a
Source: Shivangi
We can see a picture of what you could interpret as a clock tower with a “waterfall.” However, this picture is filled with shapes that cannot exist in the natural world. It is filled with impossible shapes. What is precisely an impossible object, and why does this look like a building that could have existed in the real world until we take a closer look? In these sets of illusions, issues of depth and size play an important role.
An impossible object is an object that cannot occur according to established physical laws but has a characterization or depiction that makes it appear plausible at first glance. It consists of a two-dimensional figure that the visual system quickly and subconsciously interprets as a projection of a three-dimensional object. After a few seconds of examining the figure, the impossibility becomes obvious. However, the initial impression of a 3D item persists even after it is refuted.
Impossible objects come under the branch of cognitive illusions. Unlike those with a physical or physiological foundation, cognitive illusions emerge when stored knowledge and assumptions are misdirected. The illusion is perceptual, yet it is within conscious control to some extent (It is possible to reverse cognitive illusions at one’s will).
Ambiguous illusions and paradox illusions are types of cognitive illusions. Ambiguous illusions occur when visual information cannot confirm a single view, causing an image or object to shift in appearance. The switch is perceptual, implying that the mind is involved in the interpretation. The Necker cube (simple wired symmetrical cube) is a famous example. In this Necker cube, the cube face in the front shifts to the back when more attention is paid to the backface.
In contrast, paradox illusions feature items that would be hard to build as continuous objects, such as the Penrose triangle or the impossible staircases depicted in M. C. Escher’s work. The illusion of the impossible triangle is based on a cognitive mistake that adjoining edges must join. Perceptual learning produces such illusions as a side effect. Perceptual learning is the improvement of our ability to make sense of what we see, hear, feel, taste, or smell because of our experiences. It is a bottom-up process that is permanent or semi-permanent, where we use our previous experience to make sense of the world around us.
We will be looking at six different types of impossible figures and examining how each of them is perceived by our brains. The six impossible figures would be Penrose Triangle and stairs, Neckner’s cube, Impossible cube, Devil’s fork, and Escher’s waterfalls.

Figure 8.3.b
Source: Shivangi
We will first examine Penrose Triangle (also known as Tribar or impossible triangle), Penrose stairs and Escher’s waterfalls. The Penrose triangle and stairs were designed by Oscar Reutersvärd from Sweden, popularised by Roger Penrose, and eventually featured extensively in the works of M. C. Escher.
The Penrose triangle seems to be a two-dimensional representation of a three-dimensional triangle made of square beams. However, any 3D object cannot achieve the properties of this 2D depiction. The Impossible Triangle cannot exist
because the principles of Euclidean geometry would have to be broken for it to exist. For example, the bottom bar of the tribar is spatially present in front of and behind the uppermost point of the tribar.
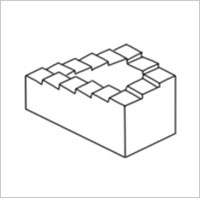
Figure 8.3.c
Source: Shivangi
The Penrose Stairs is a two-dimensional staircase with four 90-degree turns forming a continuous loop. The stairwell could potentially be climbed or descended endlessly without ever reaching its destination. Perspective distortion is the source of this illusion.

Figure 8.3.d
Source: Shivangi
The Escher waterfall is made up of two Penrose triangles. The water at the waterfall’s base appears to flow downhill, and if one follows the water’s path until it reaches the end, it seems to be at the peak of the waterfall. These illusions rely on the perception of two-dimensional images as three-dimensional objects by the human eye. The illusion of a three-dimensional object that cannot possibly exist is created by distorting visual perspective. A problem develops because perceptual learning instructs us that adjoining edges must be connected. Moreover, we also believe that features that seem touching in 2D must be at the same distance from us as viewers. The illusion is further enhanced using perspective to generate depth.
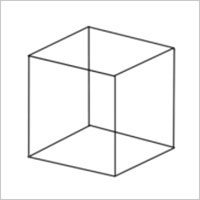
Figure 8.3.e
Source: Shivangi
The next object we will focus on will be Necker’s cube and the impossible cube. The Necker cube was invented in 1832 by Louis Albert Necker, who noticed that ambiguous cubic structures could change perspectives spontaneously. The Necker cube is a wire-frame cube with an ambiguous line design. There are no clues to detect whether one-line overlaps in front of or behind another when drawing in an isometric perspective (visually representing 3D objects as 2D). This produces an ambiguous situation in which the 3D cube can be oriented in two different ways. When viewing a representation of the Necker cube, it frequently appears to switch between the two possible interpretations (like the figures below)
Figure 8.3.f
Source: Sruthi Sridhar
Because the line drawing of the cube is ambiguous, the brain picks an interpretation of the unclear portions that make the entire figure consistent. It’s rare to encounter an inconsistent cube interpretation (the impossible cube is an example of an inconsistent interpretation). The brain chooses between two alternative perceptions in the three-dimensional world. When looking at the Necker cube, most people consider the lower-left face to be in front. This could be because people look at things from above more often than underneath. When offered a choice, the brain selects the interpretation that closely resembles daily life. There’s also evidence that the brain evaluates visual images based on previous experiences, which helps perceive depth in this illusion.
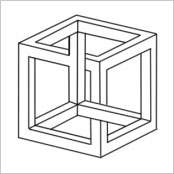
Figure 8.3.g
Source: Shivangi
The ambiguity in a Necker cube depiction is used to create the impossible cube. M. C. Escher is credited with inventing the impossible cube. A Necker cube with solid beam edges is commonly used to represent an impossible cube. Because of its apparent solidity, the impossible cube has more visual ambiguity than the Necker cube (which is less likely to be recognized as an impossible object). All the corners appear correct when looking at the impossible cube, yet the cube’s edges overlap in unexpected ways. The trick, just like the Penrose triangle, relies on the human eye’s ability to interpret two-dimensional images as three-dimensional objects. The sense of depth is created via visual perspective, even though the three edges on the back of the cube are in the front.
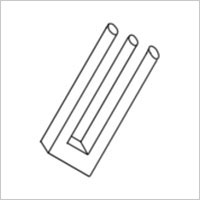
Figure 8.3.h
Source: Shivangi
Finally, we have the Devil’s fork (also known as blivet or impossible fork). D.H. Schuster is believed to have created the prong in 1964. It looks to have three cylindrical prongs on one end that unexpectedly turn into two rectangular-shaped prongs on the other end. Often, the blivet appears plausible at first glance, but upon closer scrutiny, it becomes impossible to decipher. The prongs are formed by joining lines that extend from one side to the opposite end. The illusion gets more convincing the more extended the fork’s prongs are and the further apart the two sides are.
A few fundamental questions arise when we look at shapes like these: Why do we keep seeing these figures as impossible objects even though we know they cannot exist? Why don’t we consider the figures as 2D lines on a page? Or merely as representations of other 3D objects consistent with the lines on the page? For example, if we look at the impossible cube, it initially just looks like many 2D lines on a page. However, perceptual learning recognizes these as three-dimensional objects, such as a cube in this case. Part of the solution to these questions is that our visual system is independent of our belief system, at least to some extent. Visual illusion experiences, for example, persists even when one believes one is experiencing an illusion. Like the lighting checkerboard illusion you will encounter in this course, we could only see the tiles as being different colored even after acknowledging that they are the same-colored tiles. However, that is not the complete story. The question remains: why would the visual system not change the interpretation autonomously?
Many psychologists believe the answer is that the visual system functions by strictly following specific rules, even if doing so results in inconsistency. Psychologists try to figure out these rules by studying impossible objects (and other perceptual phenomena). They believe, for example, that the visual system obeys the law of proximity when viewing the impossible triangle. If there is no apparent gap between elements portrayed in an image, they are viewed as forming a whole and connected. Therefore, the figure in the first image is not regarded as an object with shape as it lacks conjoined ends. However, when viewed from an angle, it seems like there is no obvious space between the ends, and it is regarded as an object with shape. These impossible figures are also important for the designer. While making them, you will encounter a reflexive and deep understanding of the phenomena and how it affects the experience.
• Impossible Figure......